Vajon helyesen járunk-e el, ha azt mondjuk:
Befektettünk 100 egység pénzt és kaptunk 10+10+10+10+110, azaz összesen 150 egység pénzt?
A válasz egyértelműen: NEM. Mégpedig azért nem helyes, mert alapelvként leszögeztük: „A korábban rendelkezésre álló pénz értékesebb, mint a később rendelkezésre álló.”
Ezt az elvet fejezi ki a „pénz időértéke” fogalom. A pénz időértéke azt jelenti, hogy a különböző időpontbeli pénzeknek a piacokon különböző értéke, azaz ára van. Azt mondjuk, hogy 100 forint ma többet ér, mint 100 forint holnap!
Ezért nem szabad a befektetéseket úgy értékelnünk, hogy egyszerűen összeadjuk a különböző időpontbeli pénzeket, mint ahogy azt sem mondhatjuk, hogy egy forint meg egy dollár az két „pénz”! És valóban, ez utóbbi nem is jutna eszébe senkinek. De a különböző időpontbeli pénzeket a mindennapi gyakorlatban mégis hajlamosak vagyunk kényelmesen összeadni, mondván „forint-forint”!
A különböző időpontban esedékes pénzeket csak úgy szabad összehasonlítani, ha előbb azonos időpontra, leggyakrabban a mai napra, a jelenre átszámoljuk az értéküket.
Általában elmondhatjuk, hogy egy befektetés értékét úgy értelmezhetjük, mint a hozzá tartozó pénzáramlás jelenértékét. A pénz időértékének kalkulációja az alábbi módon végezhető el:
FV = PV x(1+r)t
(tehát a jövőbeli érték a jelenérték kamatos kamattal emelt értéke), ahol
PV (present value) a jelenbeli pénz,
FV (future value) a jövőbeli pénz,
r (rate of interest) kamatláb - egységnyi tőke egységnyi idő alatti növekedésének mértéke
t időtartam mellett (kamatos kamatozás feltételezése mellett)
A pénz időértékének kalkulációja végső soron mindig ezen összefüggés alapján számítható ki. (Ezt alkalmazzuk a betétek gyarapodásának számszerűsítésekor is.)
Diszkontálásról (vagy magyarul jelenérték-számításról) beszélünk akkor, ha a jövőbeli pénz jelenbeli értékét határozzuk meg. Ez a kamatos kamatozás képletéből a PV értékének átrendezéssel kapott meghatározását jelenti ( az FV, az r és a t ismeretében) :
| PV = FV × |
1
(1+r)t |
A pénzáramlás jelenértéke (a Diszkontált Cash Flow) a különböző időpontokban esedékes pénzösszegek jelenértékeinek az összege.
A jövőbeli pénzáramlások jelenértékét a következőképpen határozhatjuk meg:
Legyen
Ct : a t. időpontban esedékes pénzösszeg, (tehát egy jövőben esedékes összeg)
t : a jelen időponthoz képest eltelt idő: t > 0, (például 5 év)
r : egy időegységre vonatkozó kamatláb. (pl.: 10 %)
Első lépés: kiszámítjuk a különböző t időpontokban esedékes Ct pénzösszegek r kamatlábbal diszkontált értékeit.
Második lépés: összeadjuk a diszkontálással megállapított jelenértékeket. Az így kapott összeget tekintjük a vizsgált pénzáramlás jelenértékének, vagy - másképpen mondva - a diszkontált cash flow értéknek:
| PV = |
n ∑ t=1 |
Ct (1+r)t |
A fentieket egy példán keresztül is nyomon követhetjük:
Legyen „A”, „B”, és „C” egy-egy befektetés jövőbeli pénzáramlása.
|
|
A
|
B
|
C
|
|
CF0
|
–400
|
–400
|
–400
|
|
CF1
|
+100
|
+200
|
+300
|
|
CF2
|
+200
|
+200
|
+200
|
|
CF3
|
+300
|
+200
|
+100
|
A Cash Flow alapján láthatjuk, hogy mindhárom vizsgált befektetés ugyanannyiba kerül (400), és mindhárom „összességében” 600-at fizet majd vissza. Nagyon fontos azonban belátni, hogy a három pénzáramlás mégsem ugyanazt kínálja számunkra, hiszen a jövőbeli kifizetések időzítése eltérő. A három befektetés közül befektetői szemszögünkből a „C” a legkedvezőbb, hiszen itt a nagyobb pénzösszegekhez hamarabb hozzájutunk.
A pénzáramlások jelenértéke éppen ezt a különbséget fogja számunkra számszerűen kifejezni. Tegyük fel, hogy a piaci kamatláb 10%. (Ezt megadhatjuk befektetői hozamelvárásként is.) Mennyit érnek számunkra az egyes befektetések? Úgy is fogalmazhatunk, hogy mekkora az egyes befektetések pénzáramlásainak jelenértéke, ha 10%-kal diszkontálunk?
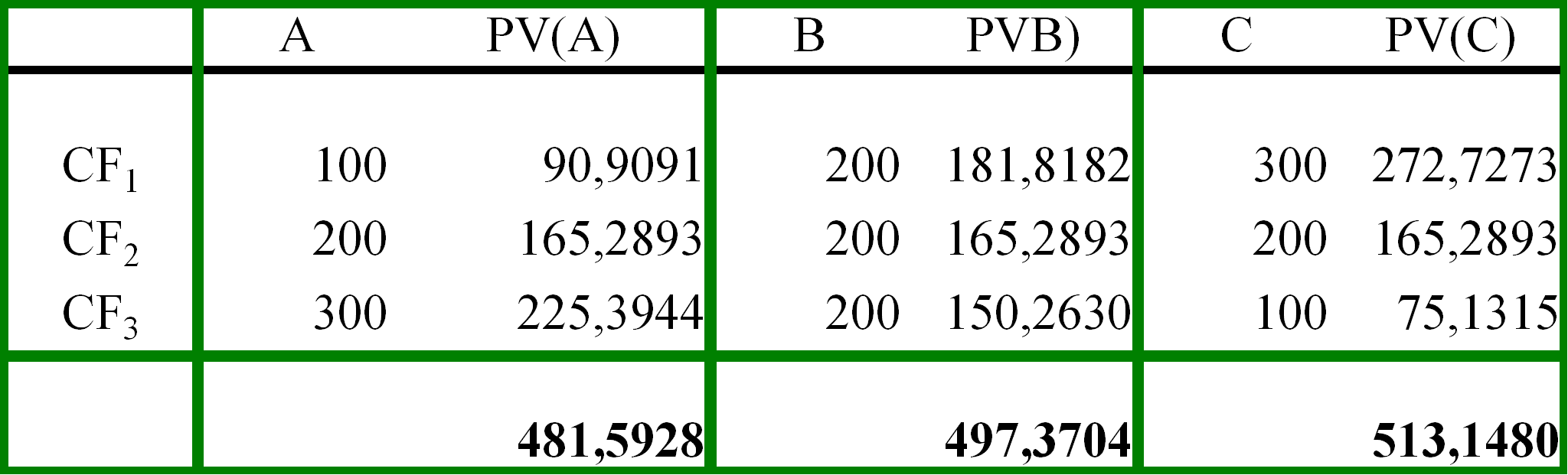
A számításokat az alábbi táblázat foglalja össze.
Az „A” befektetés jelenértékének számításához a következő műveleteket kell elvégezni:
Az első évben esedékes pénz (100) jelenértékét egy évre kell diszkontálni r=10% (azaz 0,1) kamatlábbal:
| 100 = |
90.9091
1+0.1 |
A két év múlva esedékes pénzt (200) kettő évre kell diszkontálni:
| 200 = |
165.2893
1.12 |
S végül a három év múlva esedékes pénz jelenértéke:
| 300 = |
225.3944
1.13 |
Az „A” befektetéshez tartozó pénzáramlás jelenértéke az egyes évek pénzáramlásaira számolt jelenértékek összege :
90,9091+165,2893+225,3944 = 481,5928.
A másik két befektetési pénzáramlás jelenértékét hasonlóképp kell meghatároznunk.